Материалы >> Физика >>

3. Проводники в электрическом поле. Емкость. Конденсаторы.

Проводники в электрическом поле.

При отсутствии внешнего электрического поля свободные электроны проводника совершают хаотические тепловые движения, и, значит, статистически равновероятно распределены по его объему, Суммарный заряд в любом объеме равен нулю, следовательно, электрическое поле отсутствует.

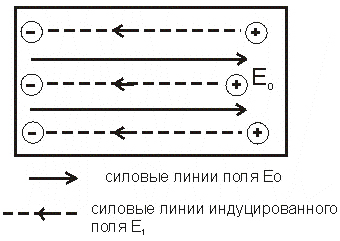
Если проводник внести в электрическое поле Ео, то свободные электроны под действием кулоновской силы сместятся против поля Ео. В результате у противоположных концов проводника скапливаются заряды противоположного знака – индуцированные заряды (рис. 8). За счет этих зарядов возникает поле:

Е₁ = – Ео        (16)

Согласно принципу суперпозиции результирующее поле с учетом условия (16) равно:

Е = Ео – Е₁ = 0

Электрическое поле внутри проводника, помещенного во внешнее электрическое поле, отсутствует.

Рис. 8. Проводник во внешнем электрическом поле Ео

Емкость. Конденсаторы.

Если проводнику сообщить заряд q, то за счет отталкивания элементарных зарядов все они расположатся на поверхности проводника. Поверхность заряженного проводника при этом будет представлять собой эквипотенциальную поверхность.

При увеличении заряда q проводника пропорционально возрастает его потенциал, т.е. q~j. Или

q = Cj            (17)

где С – коэффициент пропорциональности, который называют электроемкостью (или кратко – емкость) и измеряют в фарадах. Физический смысл емкости определяется выражением:

С = q / j       (18)

т.е. емкость проводника равна величине заряда, который увеличивает его потенциал на единицу.

Конденсатором называют систему из двух проводников, разделенных слоем диэлектрика. По форме проводников различают плоские, сферические и цилиндрические конденсаторы. На рис. 9 показан плоский воздушный конденсатор, образованный пластинами 1 и 2.

Если плоский конденсатор зарядить (на пластины 1 и 2 подать заряд +q и -q), то между пластинами образуется электрическое поле Е, величину которого согласно теореме Гаусса можно представить в виде:

      Е =  s   =   q         (19)

e_оe    e_оes

где s – поверхностная плотность заряда; e – диэлектрическая проницаемость диэлектрика, заполняющего пространство между пластинами (в данном случае воздух, для которого e = 1), s – площадь пластин. Так как величина Е в формуле (19) не зависит от расстояния между пластинами, значит, между ними Е=const, т.е. поле однородное. На рис. 9 показаны силовые линии поля Е плоскостного конденсатора.

Из (19) имеем:

q = e_оesE                (20)

Так как поле Е однородное, то:

Е = U / d,                  (21)

где U = dj - напряжение, d – расстояние между пластинами.

Из формул (20) и (21):

q = e_оesU / d            (22)

Учитывая (17), получаем емкость конденсатора:

С = e_оes / d              (23)

Из формул (22) и (23) энергию конденсатора можно представить в виде:

W = qU / 2 = q² / 2C = CU² / 2.     (24)

Рис. 9. Поле Е плоского воздушного конденсатора.

Copyright © Tehnologam.narod.ru
При перепечатке и размещении материалов сайта на других ресурсах ссылка на http://www.tehnologam.narod.ru обязательна.